
‘Art inside a material’: USask mathematician recognized for quantum research
A paper by Dr. Steven Rayan (PhD) is the finalist for a prestigious Cozzarelli Prize
By Chris PutnamAn honour from the U.S. National Academy of Sciences is the latest recognition of a University of Saskatchewan (USask) mathematician’s ground-breaking contributions to quantum science.
A paper coauthored by Dr. Steven Rayan (PhD), professor in the Department of Mathematics and Statistics in the College of Arts and Science, is the finalist—or first runner-up—for a 2022 Cozzarelli Prize.
“I think it means that we’re going in the right direction: that the work is resonating and that people are seeing the applications of it,” said Rayan.
Awarded in six categories, the Cozzarelli Prize recognizes the most significant papers published in the past year in the prestigious journal Proceedings of the National Academy of Sciences (PNAS). Winners and finalists were chosen from more than 3,200 published articles.
Rayan’s paper, titled “Automorphic Bloch theorems for hyperbolic lattices,” was co-written with physicist Dr. Joseph Maciejko (PhD) of the University of Alberta. It is part of a series of collaborations in which the two researchers have developed and refined an entirely new theory of quantum materials.
Their papers have kicked off a flurry of work around the world by other scientists attempting to fabricate the materials predicted by Rayan and Maciejko for use in new technologies.
Quantum materials are materials with unusual properties such as the ability to perfectly conduct or insulate electrical currents. They are essential ingredients for current and future quantum technologies—for example, quantum computers and quantum sensors such as next-generation MRI (magnetic resonance imaging) machines.
“I like to think of them as materials that are somehow imperfectly engineered, but under the right conditions behave perfectly,” said Rayan, who directs USask’s Centre for Quantum Topology and Its Applications (quanTA).
Engineering and fabricating “perfect” materials is very challenging. Rayan and Maciejko wondered if it might be possible to introduce imperfections in a controlled way, which could lead to materials that are easier to produce but maintain the desired behaviours.
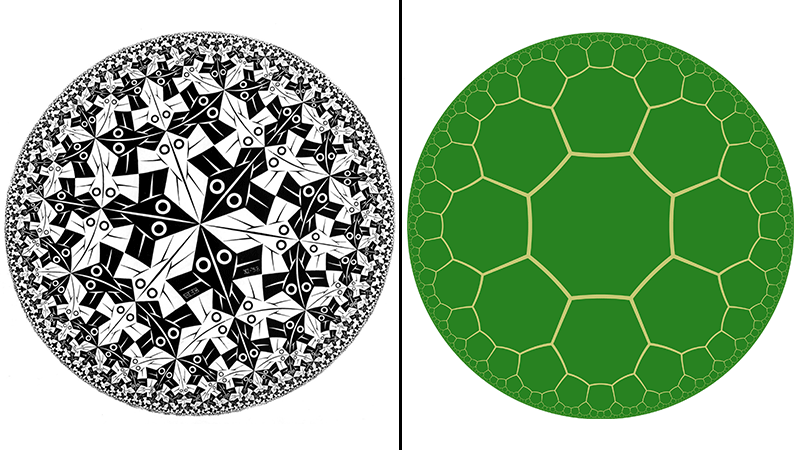
They turned to the world of art and to a classic geometry problem.
As any artist knows, only certain shapes can “tile the plane,” or cover a surface with no gaps or overlaps. Triangles, squares or hexagons with equal sides can tile the plane, but not pentagons or octagons.

The problem is important in materials science because many of the physical materials needed for sensitive electronics and quantum technologies are thin films, or two-dimensional materials, that resemble a tiled floor when examined at the quantum level.
Perfect conductivity happens when electrons can hop smoothly across these surfaces, which are nearly perfect crystals—meaning they are made up of exact copies of tiny cells repeated throughout the material.
“This crystalline nature is what makes it possible to start to design these materials from scratch, because if you can engineer behaviour in one tiny cell, then you can use mathematics to understand how to propagate this behaviour to all of the cells. You can mathematically take the behaviour and copy it from cell to cell, producing a complete material with a predictable behaviour,” said Rayan.
The imperfection introduced by Rayan and Maciejko is called a “hyperbolic geometry”: a warping of the crystal that allows shapes that couldn’t otherwise be tiled—such as octagons—to seamlessly fill a surface.
The most famous examples of hyperbolic geometry might be in the works of the Dutch artist M.C. Escher. In a series of designs, Escher tiled shapes by warping and shrinking them as they moved outward from the centre of a circle.
Rayan and Maciejko applied the same idea to quantum materials.
“The moment we started thinking, ‘Oh, we need to warp the octagons,’ (we realized) we’re in the territory of Escher now. We’re really doing it: we’re trying to put Escher’s art inside a material,” said Rayan.
That innovation was the subject of their first paper on hyperbolic band theory in 2021.
For their 2022 paper recently recognized by PNAS, the researchers took the concept to the next level. They succeeded in working out the mathematics to allow scientists to predict and control the exact behaviour of a hyperbolic material by understanding the workings of just a single cell inside it.
The same control of perfect crystals—the kind already widely used in electronics—has been possible for nearly a century thanks to mathematics established in the early 20th century by the physicist Felix Bloch. But Rayan and Maciejko’s result is the first time this level of understanding has been extended to hyperbolic crystals, making their work a 21st-century upgrade to one of the bedrocks of modern materials science.
Most significantly, their paper gives other researchers a powerful tool to engineer revolutionary new materials based on warped crystals.
“This is why this is so important. We’re saying that we can open up materials science, solid-state physics and the electronics industry—the quantum electronics industry now—to this much bigger class of materials that do not have to be 100 per cent perfect,” said Rayan.
Rayan is excited to see how other researchers use his tool to build real-world materials and technologies. He hopes the work helps cement USask and the quanTA centre as a hub for quantum science.
“I think that people may not have thought that it was possible to understand mathematically these kinds of hyperbolic materials. But we showed that we can.”

